8.2 Eksperimen Agglomerative Clustering
library (readr)
urlfile = "https://bit.ly/3VO3kRE"
data<-read.csv(url(urlfile), row.names = "Kabupaten")| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| CILACAP | 5.19 | 5.67 | 5.08 | 5.44 | 5.22 | 6.05 | 11.47 | 9.78 | 5.55 | 5.12 |
| BANYUMAS | 5.71 | 4.47 | 5.18 | 5.51 | 5.02 | 6.21 | 7.39 | 6.96 | 5.98 | 8.22 |
| PURBALINGGA | 3.30 | 2.19 | 3.80 | 3.13 | 3.73 | 3.34 | 8.71 | 7.41 | 3.21 | 4.65 |
| BANJARNEGARA | 2.73 | 2.34 | 3.76 | 2.80 | 2.57 | 2.99 | 3.31 | 5.45 | 4.21 | 6.05 |
| KEBUMEN | 4.17 | 2.55 | 3.26 | 4.16 | 3.15 | 4.15 | 4.30 | 9.29 | 4.61 | 4.34 |
| PURWOREJO | 1.87 | 2.12 | 1.48 | 3.05 | 1.78 | 1.83 | 5.00 | 4.90 | 3.12 | 2.09 |
| WONOSOBO | 2.13 | 1.95 | 3.00 | 1.78 | 1.62 | 2.06 | 0.45 | 2.32 | 3.57 | 0.84 |
| MAGELANG | 3.95 | 3.01 | 4.22 | 4.15 | 3.01 | 3.64 | 1.44 | 3.35 | 5.69 | 3.67 |
| BOYOLALI | 2.19 | 3.07 | 1.61 | 2.74 | 2.11 | 1.82 | 1.71 | 2.34 | 3.41 | 1.55 |
| KLATEN | 3.84 | 5.15 | 1.93 | 4.64 | 4.04 | 3.78 | 8.71 | 4.45 | 3.99 | 3.09 |
Standarisasi Data
Sebelum melakukan analisis clustering, penting untuk menstandarisasi data agar setiap fitur memiliki skala yang sama. Standarisasi membantu menghindari bias yang mungkin muncul akibat perbedaan skala antar fitur, yang dapat mempengaruhi hasil analisis, terutama dalam pengukuran jarak.
Dalam R, kita dapat menggunakan fungsi scale() untuk menstandarisasi dataset. Fungsi ini mengubah setiap fitur dalam dataset sehingga memiliki rata-rata 0 dan deviasi standar 1. Proses ini dilakukan dengan cara mengurangi rata-rata dari setiap nilai dan membaginya dengan deviasi standar fitur tersebut.
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| CILACAP | 1.4450108 | 1.6357957 | 1.0041319 | 1.6983202 | 1.3694832 | 1.7177332 | 3.2150170 | 2.4732171 | 1.5722235 | 0.8644476 |
| BANYUMAS | 1.7671470 | 0.9380866 | 1.0492817 | 1.7443527 | 1.2535376 | 1.8038274 | 1.6920805 | 1.4657198 | 1.8233322 | 2.0488467 |
| PURBALINGGA | 0.2741697 | -0.3875608 | 0.4262142 | 0.1792452 | 0.5056885 | 0.2595125 | 2.1847953 | 1.6264906 | 0.2057255 | 0.6848774 |
| BANJARNEGARA | -0.0789411 | -0.3003472 | 0.4081543 | -0.0377655 | -0.1667960 | 0.0711815 | 0.1691441 | 0.9262442 | 0.7896990 | 1.2197673 |
| KEBUMEN | 0.8131283 | -0.1782481 | 0.1824052 | 0.8565817 | 0.1694462 | 0.6953645 | 0.5386801 | 2.2981555 | 1.0232884 | 0.5664375 |
| PURWOREJO | -0.6117047 | -0.4282605 | -0.6212614 | 0.1266366 | -0.6247812 | -0.5530016 | 0.7999682 | 0.7297465 | 0.1531679 | -0.2932070 |
| WONOSOBO | -0.4506367 | -0.5271026 | 0.0650157 | -0.7085259 | -0.7175376 | -0.4292411 | -0.8984045 | -0.1920063 | 0.4159560 | -0.7707873 |
| MAGELANG | 0.6768400 | 0.0892071 | 0.6158435 | 0.8500056 | 0.0882843 | 0.4209392 | -0.5288685 | 0.1759803 | 1.6539798 | 0.3104545 |
| BOYOLALI | -0.4134671 | 0.1240926 | -0.5625667 | -0.0772220 | -0.4334709 | -0.5583825 | -0.4280859 | -0.1848610 | 0.3225202 | -0.4995217 |
| KLATEN | 0.6086958 | 1.3334551 | -0.4180873 | 1.1722336 | 0.6854041 | 0.4962716 | 2.1847953 | 0.5689757 | 0.6612249 | 0.0888572 |
Ukuran Similarity dan Dissimilarity
Dalam analisis clustering, ukuran similarity (kesamaan) dan dissimilarity (ketidaksamaan) sangat penting untuk menentukan seberapa dekat atau jauh objek satu sama lain dalam ruang fitur. Ukuran dissimilarity sering digunakan untuk mengukur jarak antara data point, yang kemudian digunakan dalam algoritma clustering untuk mengelompokkan data berdasarkan kedekatan mereka.
Salah satu langkah awal dalam proses clustering adalah menghitung matriks dissimilarity, yang memberikan informasi tentang jarak antara setiap pasangan objek dalam dataset. Dalam konteks ini, kita menggunakan ukuran jarak Euclidean, yang merupakan salah satu metode paling umum untuk mengukur jarak antara dua titik dalam ruang multidimensi.
Pada kode di atas, kita menggunakan fungsi dist() dari R untuk menghitung matriks dissimilarity. Parameter df merujuk pada data yang telah distandarisasi, yang berarti bahwa setiap fitur dalam dataset telah dinormalisasi untuk memiliki rata-rata 0 dan deviasi standar 1. Proses standarisasi ini penting untuk memastikan bahwa semua fitur berkontribusi secara seimbang terhadap perhitungan jarak, terutama ketika fitur memiliki skala yang berbeda.
Setelah menghitung matriks dissimilarity menggunakan fungsi dist(), kita sering kali ingin melihat representasi matriks tersebut dalam format yang lebih mudah dibaca. Dalam R, kita dapat menggunakan fungsi as.matrix() untuk mengonversi objek dissimilarity menjadi matriks biasa. Ini memungkinkan kita untuk melihat nilai-nilai jarak antara objek-objek dalam dataset.
Pada kode di atas, res.dist adalah objek dissimilarity yang telah dihitung sebelumnya. Dengan menggunakan as.matrix(res.dist), kita mengonversi objek tersebut menjadi matriks. Kemudian, kita menggunakan indeks [1:5, 1:5] untuk menampilkan lima baris dan lima kolom pertama dari matriks dissimilarity.
as.matrix(res.dist)[1:5, 1:5]
#> CILACAP BANYUMAS PURBALINGGA BANJARNEGARA KEBUMEN
#> CILACAP 0.000000 2.327193 3.828424 5.188508 3.891360
#> BANYUMAS 2.327193 0.000000 3.809719 4.232529 3.310710
#> PURBALINGGA 3.828424 3.809719 0.000000 2.418211 2.235801
#> BANJARNEGARA 5.188508 4.232529 2.418211 0.000000 2.159694
#> KEBUMEN 3.891360 3.310710 2.235801 2.159694 0.000000Melakukan Pengelompokan Hierarkis
Setelah menghitung matriks dissimilarity, langkah selanjutnya dalam analisis clustering adalah menerapkan algoritma pengelompokan hierarkis. Dalam R, kita dapat menggunakan fungsi hclust() untuk melakukan ini. Salah satu metode yang umum digunakan dalam pengelompokan hierarkis adalah metode Ward, yang bertujuan untuk meminimalkan varians dalam setiap cluster yang terbentuk.
Pada kode di atas, res.dist adalah matriks dissimilarity yang telah dihitung sebelumnya. Parameter method = "ward.D2" menunjukkan bahwa kita menggunakan metode Ward untuk menggabungkan cluster. Metode Ward bekerja dengan cara menggabungkan dua cluster yang menghasilkan peningkatan terkecil dalam total varians dalam cluster yang baru terbentuk. Ini membantu dalam menghasilkan cluster yang lebih homogen.
Hasil dari fungsi hclust() adalah objek yang berisi informasi tentang struktur pengelompokan hierarkis. Objek ini dapat digunakan untuk membuat dendrogram, yang merupakan representasi visual dari proses penggabungan cluster. Dendrogram ini membantu dalam menentukan jumlah cluster yang optimal dengan memotong dendrogram pada ketinggian tertentu.
Visualisasi dengan Dendrogram
Setelah melakukan pengelompokan hierarkis menggunakan metode Ward, langkah selanjutnya adalah memvisualisasikan hasil clustering untuk memahami struktur dan hubungan antar cluster. Salah satu cara yang efektif untuk melakukan ini adalah dengan menggunakan dendrogram, yang menunjukkan bagaimana objek-objek dalam dataset digabungkan menjadi cluster.
Library factoextra menyediakan fungsi yang memudahkan visualisasi hasil analisis multivariat, termasuk dendrogram untuk pengelompokan hierarkis. Berikut adalah kode untuk memvisualisasikan dendrogram dari hasil pengelompokan hierarkis yang telah dilakukan:
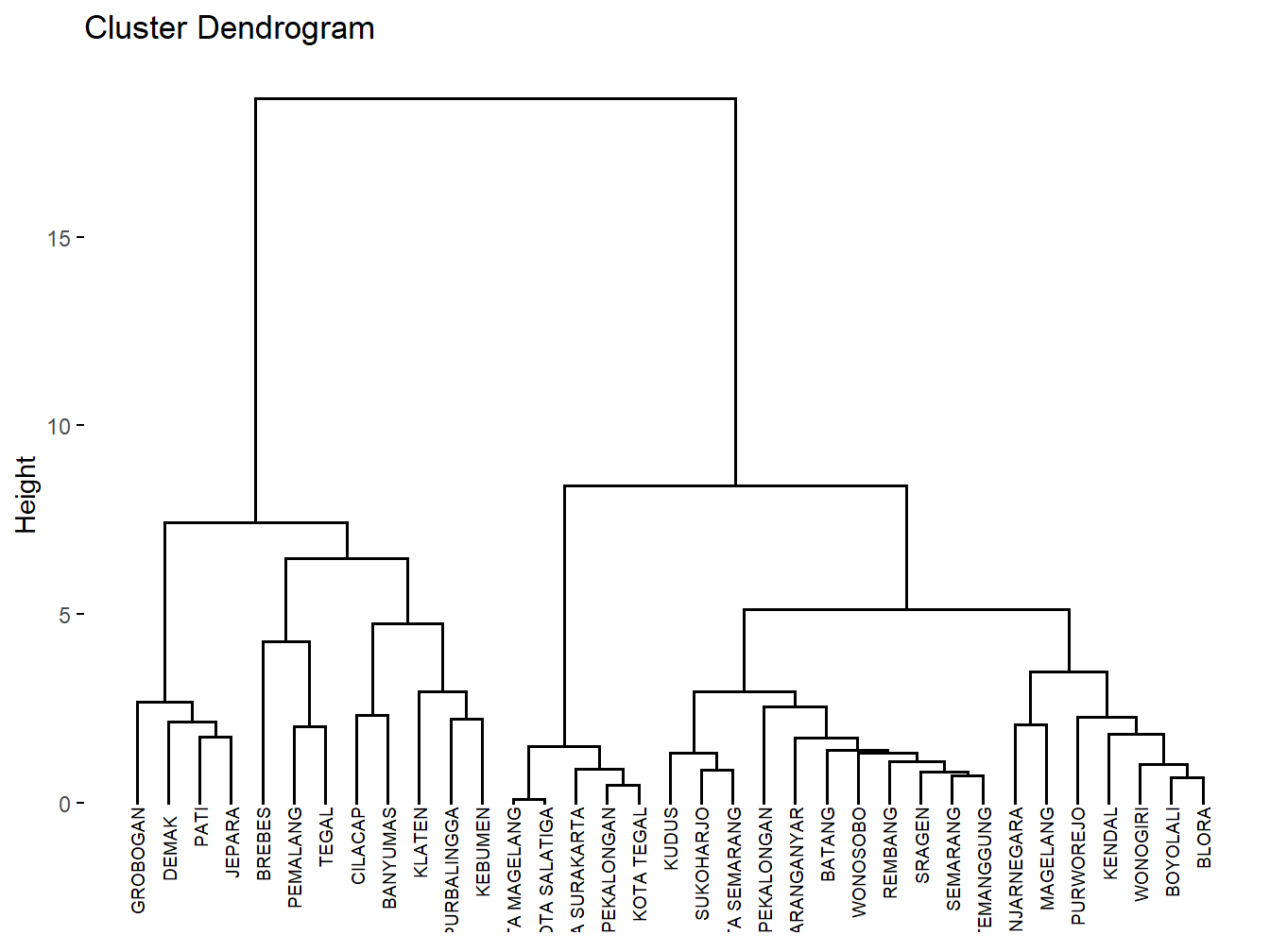
Gambar 8.1: Visualisasi Dendogram
Pada kode di atas, kita pertama-tama memuat library factoextra dan ggplot2. Fungsi fviz_dend() digunakan untuk membuat dendrogram dari objek hasil pengelompokan hierarkis res.hc. Parameter cex = 0.5 digunakan untuk mengatur ukuran label pada dendrogram, sehingga label lebih mudah dibaca.
Visualisasi dengan Dendrogram
Setelah memvisualisasikan dendrogram dari hasil pengelompokan hierarkis, langkah selanjutnya adalah menentukan jumlah cluster yang diinginkan dan memotong dendrogram untuk membentuk kelompok-kelompok tersebut. Dalam contoh ini, kita akan memotong dendrogram menjadi dua kelompok.
Fungsi cutree() digunakan untuk memotong dendrogram dan mengelompokkan objek-objek ke dalam jumlah cluster yang ditentukan. Berikut adalah kode untuk memotong dendrogram menjadi dua kelompok:
Pada kode di atas, res.hc adalah objek hasil pengelompokan hierarkis yang telah kita buat sebelumnya. Parameter k = 2 menunjukkan bahwa kita ingin memotong dendrogram menjadi dua kelompok. Hasil dari fungsi cutree() disimpan dalam variabel grp, yang berisi penugasan kelompok untuk setiap objek dalam dataset.
Jumlah Anggota dalam Setiap Cluster
Setelah memotong dendrogram dan mengelompokkan objek-objek ke dalam cluster, langkah selanjutnya adalah menghitung jumlah anggota dalam setiap cluster. Dalam contoh ini, kita akan menggunakan fungsi table() untuk menghitung jumlah anggota dalam setiap cluster.
Fungsi table() digunakan untuk menghitung frekuensi atau jumlah anggota dalam setiap kategori atau cluster. Berikut adalah kode untuk menghitung jumlah anggota dalam setiap cluster:
Visualisasi Dendrogram
Setelah memotong dendrogram untuk membentuk kelompok, kita dapat memvisualisasikan hasil pengelompokan dengan menandai setiap kelompok menggunakan warna yang berbeda. Ini membantu dalam memahami struktur cluster dan memudahkan interpretasi hasil.
fviz_dend(res.hc, k =2,
cex = 0.5,
k_colors = c("#E7B800", "#FC4E07"),
color_labels_by_k = TRUE,
rect = TRUE
)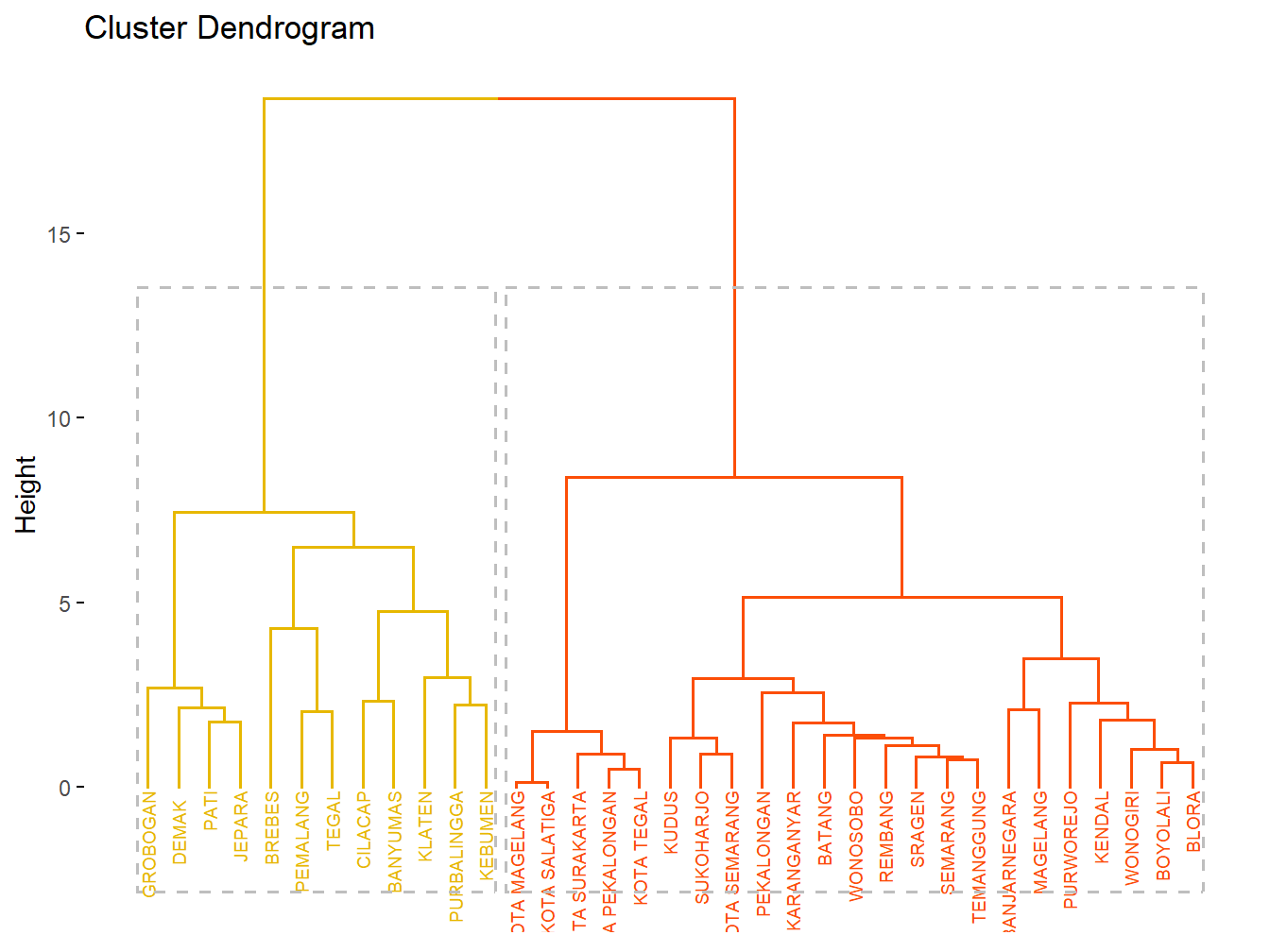
Gambar 8.2: Visualisasi Dendogram
Pada kode di atas, kita menggunakan fungsi fviz_dend() untuk membuat dendrogram dari objek hasil pengelompokan hierarkis res.hc. Parameter yang digunakan adalah sebagai berikut: k = 2 Menunjukkan bahwa kita ingin memotong dendrogram menjadi dua kelompok. cex = 0.5 Mengatur ukuran label pada dendrogram agar lebih mudah dibaca. k_colors = c("#E7B800", "#FC4E07") Menentukan warna yang akan digunakan untuk masing-masing kelompok. Dalam hal ini, kelompok pertama akan berwarna kuning (#E7B800) dan kelompok kedua berwarna oranye (#FC4E07).color_labels_by_k = TRUE Mengatur agar label pada dendrogram diwarnai sesuai dengan kelompok yang ditentukan. rect = TRUE Menambahkan kotak di sekitar kelompok untuk menyoroti batasan antar cluster.
Visualisasi Hasil Clustering
Setelah melakukan pengelompokan data dan mendapatkan penugasan kelompok untuk setiap objek, langkah selanjutnya adalah memvisualisasikan hasil clustering. Visualisasi ini membantu kita memahami distribusi objek dalam setiap cluster dan bagaimana cluster tersebut terpisah satu sama lain.
Pada kode di bwah, kita menggunakan fungsi fviz_cluster() untuk membuat visualisasi clustering. Parameter yang digunakan adalah sebagai berikut:
list(data = df, cluster = grp):Menyediakan data yang telah distandarisasi (df) dan penugasan kelompok (grp) yang dihasilkan dari pemotongan dendrogram.palette = c("#E7B800", "#FC4E07"): Menentukan warna yang akan digunakan untuk masing-masing cluster. Dalam hal ini, cluster pertama akan berwarna kuning (#E7B800) dan cluster kedua berwarna oranye (#FC4E07).ellipse.type = "convex": Menambahkan elips konsentrasi di sekitar setiap cluster, yang memberikan gambaran visual tentang sebaran objek dalam cluster.repel = TRUE: Menghindari tumpang tindih label pada plot, meskipun ini dapat memperlambat proses rendering.show.clust.cent = FALSE: Menentukan untuk tidak menampilkan pusat cluster pada visualisasi.ggtheme = theme_minimal(): Menggunakan tema minimal untuk plot, yang memberikan tampilan yang bersih dan profesional.
fviz_cluster(list(data = df, cluster = grp),
palette = c("#E7B800", "#FC4E07"),
ellipse.type = "convex",
repel = TRUE,
show.clust.cent = FALSE, ggtheme = theme_minimal())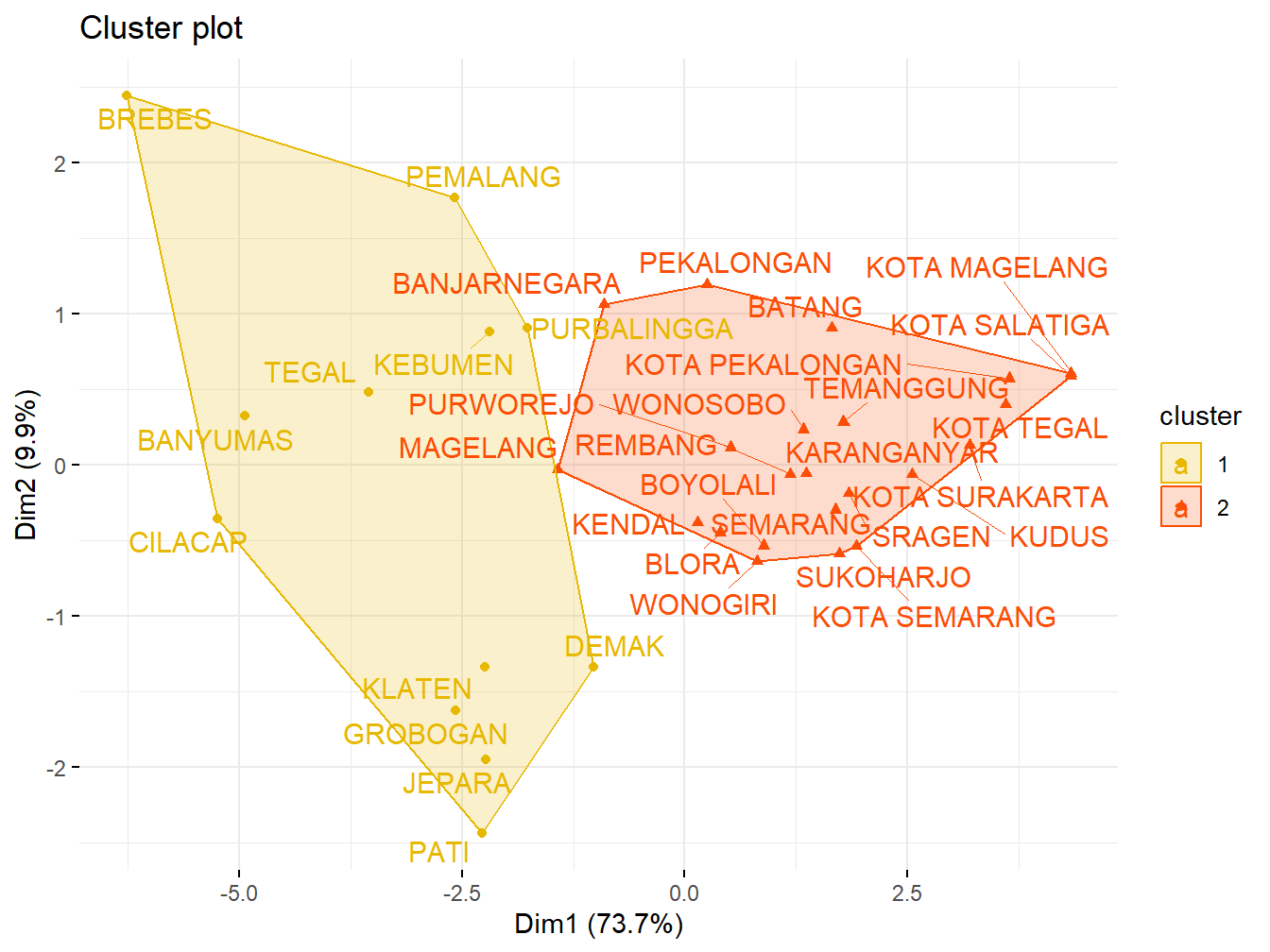
Gambar 8.3: Visualisasi Hasil CLustering